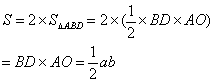教学过程设计

问题与情境

师生行为

设计意图

【活动1】

（1）    矩形是一种特殊的平行四边，它有哪些性质？

（2）    操作：请同学拿出准备好的纸片，对折两次，折出一个直角，剪一刀，得一个直角三角形，把所得的直角三角形展开，得一个四边形。

思考：观察所得的四边形，它是一个怎么样的四边形？

（3）引出菱形的概念：

学生复习矩形的有关性质.

教师明确矩形是平行四边形，所以除了具备平行四边形所有的性质，还有自己独特的性质：四个角都是直角及对角线相等.

学生实际操作，得出一个四边形

（2）平行四边形

教师提问：什么样的平行四边形？

学生：一组邻边相等

所以

得出菱形的概念：有一组邻边相等的平行四边形.

现实应用：学生举例

          教师展示图片

学生对矩形的在认识，是对矩形性质的深入理解

通过动手操作，使学生对菱形有一个感性认识，同时培养学生养成一边动手、一边思考的良好习惯

使学生感受数学的美

问题与情境

师生行为

设计意图

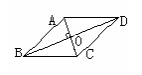
【活动2】

 （1）观察得到的菱形（如下图），它是轴对称图形么？有几条对称轴？

学生：菱形是轴对称图形，它有两条对称轴，这两条对称轴是菱形的对角线

通过动手折叠发现对称轴

【活动3】

问题：通过活动2同学们也发现了，对交线就是菱形的 对称轴，那么沿着对称轴折叠，你们能得出哪些结论？并说明理由

教师强调：证明的方法可以是三角形全等，还可以是等腰三角形三线合一的性质，方法不唯一

分四个同学一小组，讨论得出结论：AB=BC=CD=DA，

   OA=OC，OB=OD，

   AC⊥BD，   

 ∠DAC=∠BAC=∠DCA=∠BCA=∠DAB=∠DCB

∠ADB=∠CDB=∠ABD=

∠CBD=∠ADC= ∠ABC

以上这些结论也就是菱形的性质：

(1)   菱形的四条边都相等

（2）菱形的两条对角线互相垂直，并且每一条对角线平分一组对角。

（3）注意：具备平行四边形所有的性质

让学生小组合作经历观察、讨论、归纳的过程，培养学生分析图形的能力

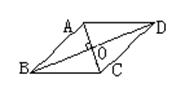
【活动4】例1、如图，菱形花坛ABCD的周长为80m，∠ABC=60度，沿着菱形的对角线修建了两条小路AC和BD，求两条小路的长和花坛的面积（分别精确到0.01m和0.01m）

【活动5】

（3）    菱形的周长

探索：

（4）菱形的面积公式是什么？如何证明这个公式？（提示：四个全等的直角三角形。）

【活动6】

练习：教科书98页 1题

作业：教科书102页5题

评价与反思

小结：通过探究，本节课你学到了哪些结论？有哪些认识？

教师引导学生分析解题思路.

（1）菱形的四边相等，已知周长则可算边长.（2）菱形的两条对角线互相垂直，并且每一条对角线平分一组对角，所以根据特殊角可算出AO、BO的长那么对角线的长也可算出。是四个全等的三角形，只要算出一个三角形的面积，那么整个菱形的面积就是它的4倍.

3）菱形的周长=边长的4倍

（4）菱形的面积公式：平行四边形的面积公式

菱形的面积公式是：

其中a、b是菱形的两条对角线分别的长）．即：“菱形的面积等于它的两条对角线长的积的一半”．

1．已知菱形的两条对角线分别是6cm和8cm ，求菱形的周长和面积．

补充练习

2．已知菱形ABCD的周长为20cm，且相邻两内角之比是1∶2，求菱形的对角线的长和面积．

学生反思学习的过程

教师的评价与反思：

（1）    菱形的性质探究是难点，所以教师在引导学生时应思路清晰，层层递进。

（2）    本节课的内容多，学生提前做好准备

（3）    练习的配备有简单到难

（4）    作业设计合理

从简单的实际问题出发，让学生体会菱形的性质，用数学方法解决实际问题，从而达到“学数学，用数学”的目的，进一步培养学生解决问题的能力.

让学生会用菱形独特的计算面积的方法

会用菱形的性质

两种不同的计算菱形面积的公式