2018-2019学年第一学期高二数学圆锥曲线复习试卷

英德市第二中学  组卷人：邹妍   审核人：阮少华 刘良滨

1、基本概念：

1、已知椭圆的方程为，求下列问题

（1）焦点在______轴，a=____,b=____,c=____,长轴长为____,短轴长为_____,焦距为____，焦点坐标___________,

顶点坐标___________________________________

（2）画出图形，并画出焦点和准线：                  

（3）离心率e=_____,e的范围是____________,e与的关系是_______________（4）准线方程为_________

变式：方程改为：、求上面的问题

2、已知双曲线的方程为 ，求下列问题

（1）焦点在______轴，a=____,b=____,c=____,实轴长为____,虚轴长为_____,焦距为____，焦点坐标___________

顶点坐标_________________，离心率e=_____,e的范围是____e与的关系是_______________

（2）画出图形，并画出焦点和准线：：

（3）准线方程为______________（4）渐近线方程为_________________

（4）变式：方程改为：、求上面的问题

3、已知抛物线方程，回答下列问题

（1）对称轴为_______,开口方向为________（2）画出图形，并画出焦点和准线：

（3）2p=______,p=______  （4）焦点坐标__________,准线方程___________（5）焦半径|PF|=__________

（5）变式：、，

题型一：定义的运用

1.椭圆上一点P到一个焦点的距离为5，则P到另一个焦点的距离为（   ）

A.5          B.6         C.4          D.10

2.动点P到点A(0，2)的距离比到直线l:y=-4的距离小2，则动点P的轨迹方程为

A.          B.       C.       D.

3.方程表示的曲线是          

4.若抛物线上一点到其焦点的距离为，则点的坐标为（    ）。

A．   B．  C．  D．

题型二：圆锥曲线焦点位置的判断（首先化成标准方程，然后再判断）：

椭圆：由分母的大小决定，焦点在分母大的坐标轴上。

双曲线：由系数的正负决定，焦点在系数为正的坐标轴上；

抛物线：焦点在一次项的坐标轴上，一次项的符号决定开口方向。

1.当k为何值时,方程表示的曲线：

(1)是椭圆；                           (2)是双曲线.

2.方程x2+(k-1)y2=k+1表示焦点在x轴上的双曲线，则k的取值范围是  （    ）

A.k＜-1                      B.k＞1

C.-1＜k＜1                   D.k＜-1或k＞1

题型三，求标准方程

1. 中心在原点，长轴长是短轴长的2倍，一条准线方程是x=4，则此椭圆的方程是_______
2. 过点A（-1，-2）且与椭圆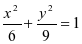的两个焦点相同的椭圆标准方程是______.

3.已知椭圆的两个焦点坐标是F1（-2，0），F2（2，0），并且经过点P（），则椭圆标准方程是______.

4.过点P（，-2），Q（-2，1）两点的椭圆标准方程是______.

5.双曲线的焦点在y轴上，且它的一个焦点在直线5x-2y+20=0上，两焦点关于原点对称，，则此双曲线的方程是_______________

6.已知双曲线经过点M（2，3），N（-7，6），则双曲线标准方程是______.

7.已知双曲线的焦点F1（-4，0），F2（4，0），且经过点M（2，2）的双曲线标准方程是______.

8.中心在原点的等轴双曲线过点M（1，3），则此双曲线方程为______.

9.中心在原点，实轴在x轴上，它的一个焦点在直线5x-2y+20=0上，离心率等于，则此双曲线方程是______.

10.已知双曲线的一个焦点F1（0，6），且与双曲线x2-2y2=2有相同的渐近线，则此双曲线方程是______.

11．双曲线的渐近线方程为，焦距为，这双曲线的方程为_______________。

12．双曲线与椭圆有共同的焦点，点是双曲线的渐近线与椭圆的一个交点，求渐近线与椭圆的方程___________

13．以=1的焦点为顶点，顶点为焦点的椭圆方程为______________

14．双曲线与椭圆有相同焦点，且经过点，求其方程_____________。

15.已知抛物线的焦点在直线-4=0上，则此抛物线的标准方程是_________

16．以坐标轴为对称轴，以原点为顶点且过圆的圆心的抛物线的方程是__________

题型四：圆锥曲线焦点三角形（椭圆或双曲线上的一点与两焦点所构成的三角形）问题

常利用定义和正弦、余弦定理求解、，四者的关系在圆锥曲线中的应用

1. 椭圆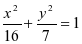的左右焦点为F1、F2，一直线过F1交椭圆于A、B两点，则△ABF2的周长为____
2. 若双曲线x2-4y2=4的焦点是F1、F2过F1的直线交左支于A、B，若|AB|=5，则△AF2B的周长是______.

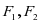3. 是椭圆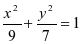的两个焦点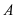，为椭圆上一点，且∠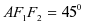，则Δ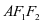的面积为（      ）         

A．     B．     C．     D．

4. F1、F2为双曲线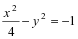的两个焦点，点P在双曲线上，且∠F1PF2=90°,则△F1PF2的面积是（   ）

A.2        B.4            C.8            D.16

5.设是双曲线的两个焦点，点在双曲线上，且，

求△的面积。

题型五：圆锥曲线中离心率

1．椭圆的离心率为，则的值为______________。

2．若椭圆的离心率为，则它的长半轴长为_______________.

3.椭圆上点P到右焦点的距离等于4，则点P到左准线的距离等于______

4.若椭圆的两焦点把两准线间的距离等分成三份，则椭圆的离心率等于（     ）

A.              B.            C.            D.

5.若双曲线两条准线间的距离的4倍等于焦距，则双曲线的离心率等于（   ）

Ａ.4             Ｂ.3             Ｃ.2               Ｄ.1

6、已知、是双曲线（）的两焦点，以线段为边作正三角形，若边的中点在双曲线上，则双曲线的离心率是（    ）

A. 　　B. 　　C. 　　D.

7．双曲线的一条渐近线与直线垂直，则这双曲线的离心率为___。

8．过双曲线的一个焦点作垂直于实轴的弦，是另一焦点，若∠，

则双曲线的离心率等于（     ）

A．   B．  C．  D．

题型六、直线与圆锥曲线

一、求弦长步骤：

1、设直线与方程；（提醒：①设直线时分斜率存在与不存在；②设为y=kx+b与x=my+n的区别）

2、设交点坐标；（提醒:之所以要设是因为不去求出它,即“设而不求”）

3、联立方程组；

4、消元韦达定理；（提醒：抛物线时经常是把抛物线方程代入直线方程反而简单）

5、弦长公式：

1.已知椭圆,过右焦点F2的直线l交椭圆于A、B两点，若|AB|=，则直线l的方程是：______.

2.已知双曲线,过它的焦点且垂直于x轴的弦长是______.

3.已知顶点在原点，焦点在轴上的抛物线被直线截得的弦长为，求抛物线的方程。

二、直线与圆锥曲线交点情况

1.直线y=x+k与椭圆相交于不同两点，则实数k的取值范围是______.

2.过点(0，3)作直线l，若l与双曲线＝１只有一个公共点，这样的直线l共有（   ）

Ａ.一条           Ｂ.二条           Ｃ.三条          Ｄ.四条

3．若直线与抛物线交于、两点，若线段的中点的横坐标是，则______。

4．若直线与双曲线始终有公共点，则取值范围是             。

5．已知，抛物线上的点到直线的最段距离为__________。

三、圆锥曲线的中点弦问题：

韦达定理：

点差法：带点进圆锥曲线方程，做差化简,得到中点坐标比值与直线斜率的等式关系

1.若直线与抛物线交于、两点，则线段的中点坐标是______。

2.已知直线l与抛物线交于A、B两点，且l经过抛物线的焦点F，A点的坐标为(8，8)，则线段AB的中点到准线的距离是A.             B.             C.          D.25

3.直线y=kx-2与抛物线交于A、B两点，且AB的中点横坐标为2，则k的值是
A.-1            B.2              C.-1或2         D.以上都不是

4、双曲线x2－4y2=4的弦AB－被点M(3,-1)平分,求直线AB的方程.